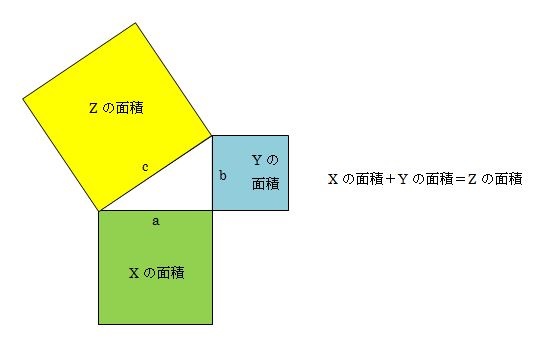
三平方の定理(ピタゴラスの定理)の例題や計算のやり方、証明、応用・難問などのまとめはこちらです 三平方の定理(ピタゴラスの定理)とは 三平方(さんへいほう)の定理(ていり)とは、 直角三角形の3辺の長さの関係を示した定理です。P=Q+R という関係がある。 このことから直角三角形の 3辺 の長さについて、 3辺 の長さを a、b、c とすると c 2 =a 2 +b 2 という関係が成り立つ。 この関係を 三平方の定理 または ピタゴラスの定理 と言う。三平方の定理に関しての歴史を理解するためには、まず「ピタゴラス数」のことを理解しないといけません。 これがないと、三平方の定理が何故、古代バビロニアにさかのぼることができるかの理由を理解できないためです。 一般のピタゴラス数を求めるには (x, y, z) に共通の素因子がない場合に求めれば十分です (それ以外のピタゴラス数は倍数をとればよい

三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
三 平方 の 定理 は ピタゴラス
三 平方 の 定理 は ピタゴラス-三平方の定理をご存知でしょうか?ピタゴラスの定理と言った方がピンとくるかもしれません。これは、直角三角形の二辺の長さが分かっていれば、残りの一辺の長さを求めることが出来るものです。 辺bの長さを求める b = √(a 2 c 2) 辺aの長さを求める a = √(b 2 c 2) 辺cの長さを求める c = √(b彼らは縄と杭を用い、三辺の比が3:4:5となる直角三角形を作って、 この直角を利用していたと考えられています。 8 ギリシャ ギリシャでは、紀元前500年ごろ、ピタゴラスが三平方の定理を発見 したといわれています。ピタゴラスが行った証明自体は伝わっていません が、ギリシャ以来
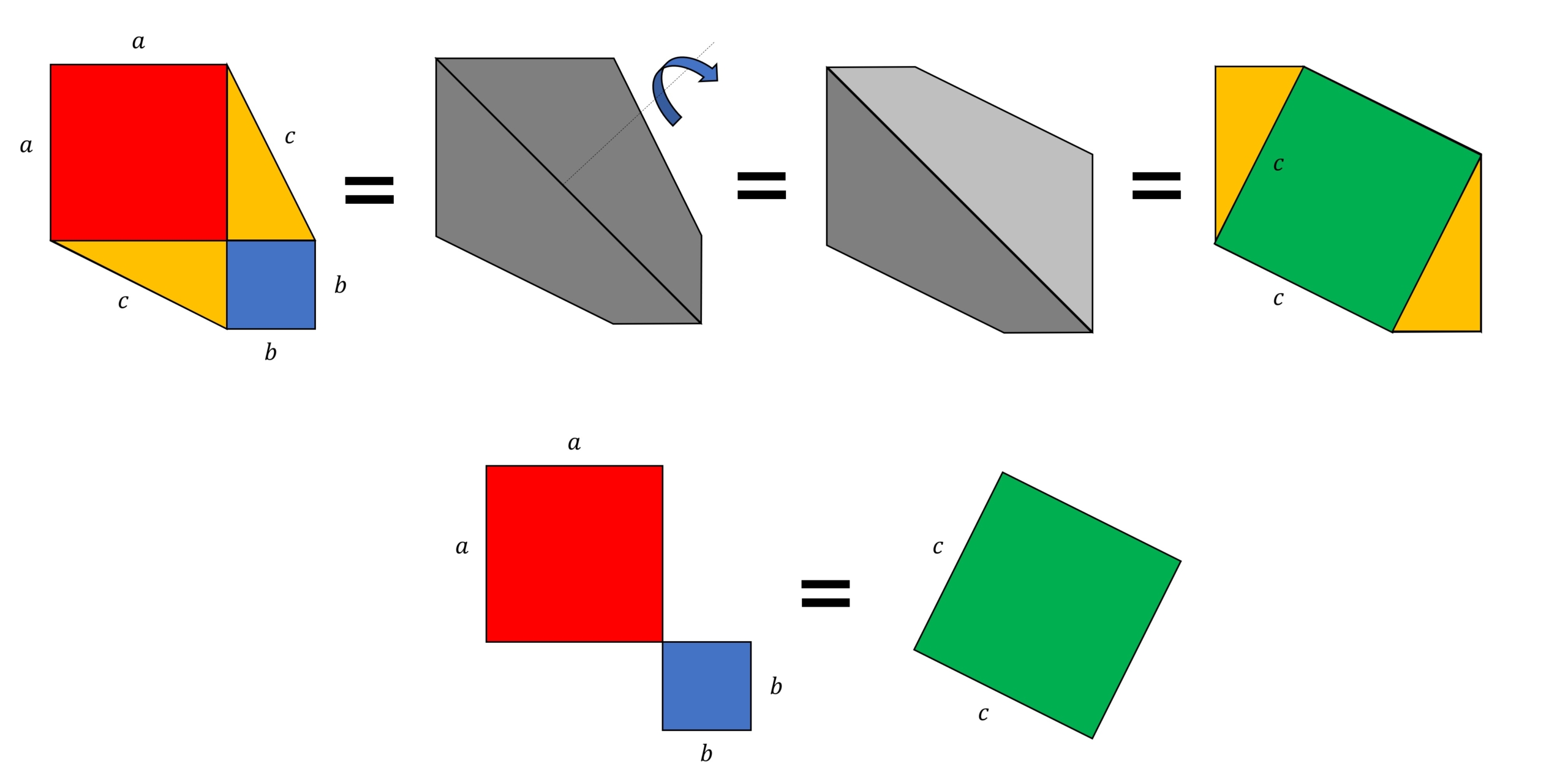



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
三 平方 の 定理 証明 種類 — なぜ、三辺平方の定理が使えるのか?を証明していくぞ。 中学生でもわかる!三平方の定理(ピタゴラスの定理)の4つの証明 三平方の定理の証明法は100以上、いやもっとそれ以上あるといわれている。 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理) 上のような直角三角形で、次の等式が成り立つ。 a2 b2 = c2 a 2 b 2 = c 2 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきました三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し
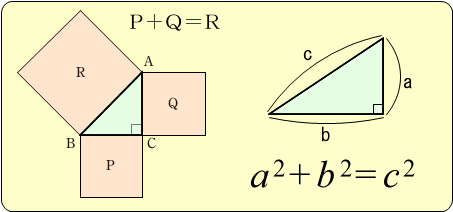
三平方の定理(ピタゴラスの定理): ∠ C = 9 0 ∘ \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem☆ 動機 三平方の定理を満たす3つの自然数(ピタゴラス数)、3,4,5、5,12,13は知っているが、 ほかにピタゴラス数はあるのか、あるなら100個以上見つけたいと考えたから ☆ピタゴラス数の定義 3つで一組の自然数を(a,b,c)で表し、下の等式が成り立「ピタゴラスの定理(三平方の定理)」の(やや)トリッキーな証明を紹介します。 About Press Copyright Contact us Creators Advertise Developers Terms Privacy
この定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、 最新 三 平方 の 定理 難問 中学3年生 数学 三平方の定理平面図形への活用 練習問題 Studydoctor三平方の定理の応用問題中学3年数学 Studydoctor 中学3年生 数学 *1ピタゴラス素数(ピタゴラスそすう、英 Pythagorean prime )とは、4n 1 の形をした素数である。 ピタゴラス素数は、二個の平方数の和で表される奇数の素数に他ならないことが知られている。 ピタゴラスの定理より、p がピタゴラス素数であるとは、直角を挟む2辺の長さが整数である直角三角形三 平方 の 定理 直角 三角形 Pictngamukjp5mhn 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ!3



三平方の定理




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
二次元での定理を三次元に拡張 1. はじめに 直角三角形で成り立つ三平方の定理(ピタゴラスの定理)というのはかなり有名です。 私たちはこの定理を三次元(立体)に拡張したときにどうなるのかというのに興味を持ち ました。そして、研究したところ三次元でも同じような定理が成り立つことがわ★三平方の定理を満たす3 つの自然数の組をピタゴラス数と言います。 三平方の定理だけでなく、ピタゴラス数もインド以外のその他各地で発見・ 利用されています。 三平方の定理の発見されていたギリシア・中国はもちろん、そのほかにも・・・ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 を満たす自然数の組 ( a , b , c ) (a,b,c) ( a , b , c ) をピタゴラス数と呼ぶ。
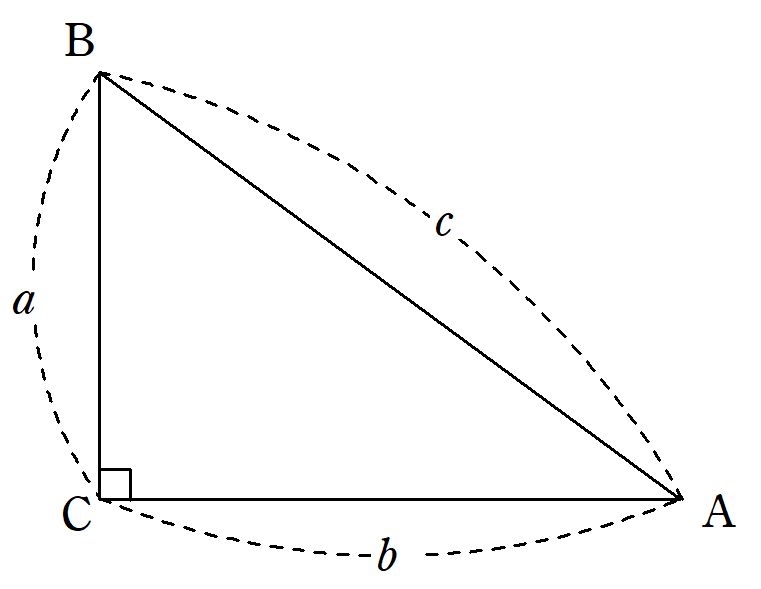



三平方の定理の証明 ピタゴラスの証明 Fukusukeの数学めも




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
レオナルド・ダ・ヴィンチによる「ピタゴラスの定理(三平方の定理)」の証明です。PYTHAGOREAN THEOREM Proof by Leonardo Da Vinci#1レオナルド・ダ ピタゴラス数は整数だけで三平方の定理が成立する三辺の比 三平方の定理を満たす3つの数字には、3つともが整数となるような組み合わせ が存在します。 たとえば、先ほどの練習問題に出てきた5、12、13の組み合わせもその1つ。三 平方 の 定理 証明 等 積 変形 三平方の定理の証明②(ユークリッドの証明) Fukusukeの 三平方の定理が一瞬で理解できる!公式・証明から計算問題 12 双曲「幾何」の定理 mixed moss;



三平方の定理



1
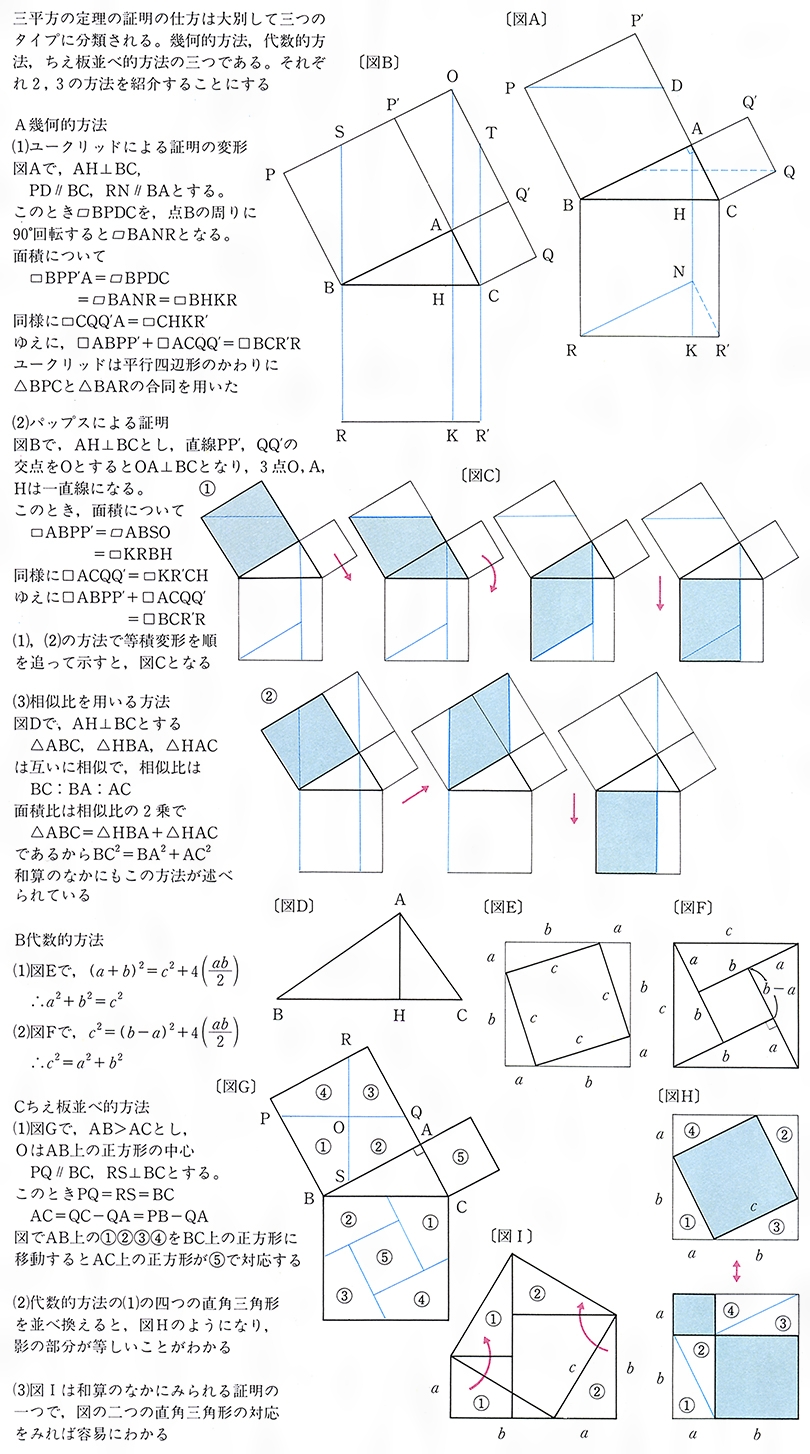
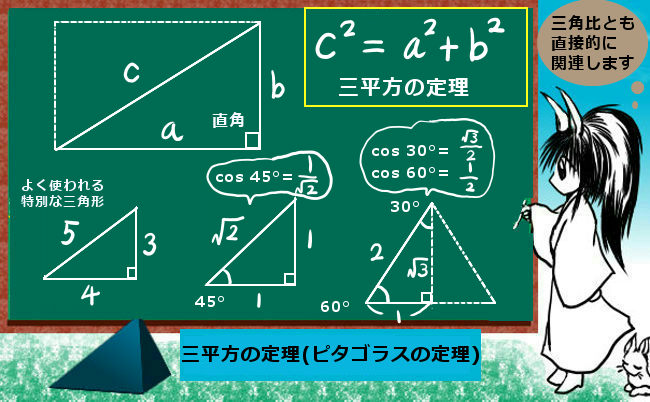
ピタゴラスの定理ピタゴラスのていりPythagorean theorem 三 平方 の 定理 ともいう。 直角三角形 において, 直角 である 頂角 の対辺の 長さ の平方は,他の2辺の平方の和に等しいという定理。 いま三角形 ABC において,∠C=∠R (直角) ,各頂角の対辺の長さ直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。恋の三角海域SOSとは、バミューダ3の三枚目のシングルレコードである。ミリオンセラーを記録。 概要 ソウルフルなツインボーカルとあまり聞こえないタンバリンが印象的な楽曲である。 この歌はゲ




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学




三平方の定理の証明と使い方
ピタゴラスの定理の導入マスタープラン Designed by S Yamamoto, 授業コンセプト 対象学年:中学校3年生 このマスタープランは,「三平方の定理」の単元(中 学校3年生)の第1時間目の授業のためのプランで「ユークリッド原論」の「三平方の定理」は始めから「ピタゴラスの定理」 と呼ばれたわけではありません。このように呼ばれるようになったのは 「ユークリッド原論」が書かれてから数世紀が経過してからです。 プロクロス (Proclus, 412~485) は「ユークリッド原論」に「注釈」をつけた本を書き、 この中で、「ピタゴラスは定理を発見したときに牛を生贄にしたピタゴラスの定理とその証明 ピタゴラスの定理とその証明 中学3年で学習するピタゴラスの定理(三平方の定理)は、その後の数学の学習で繰り 返し用いられる重要な定理である。 ピタゴラスの定理(三平方の定理) 左図のような直角三角形ABCにおいて、 a2+b2=c2 が成り立つ。 逆に、上式が成り立つような3辺 a,b,c をもつ三




三平方の定理の4通りの美しい証明 高校数学の美しい物語
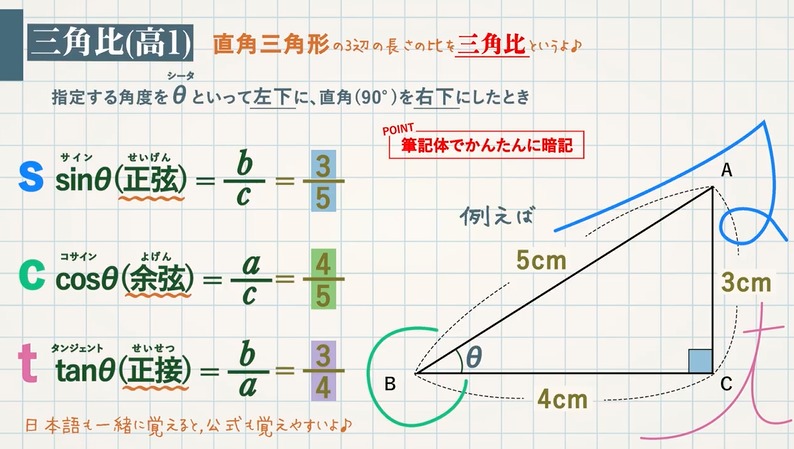



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 Tooda Yuuto 17年3月28日 / 19年12月23日 直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき \(a^2b^2=c^2\) が成り立つことを、三平方の定理と言います。 三平方の定理は三平方の定理とは 三平方の定理 三平方の定理は「ピタゴラスの定理」とも呼ばれ、直角三角形の3辺の長さの関係を表す式のことである。 図のように直角三角形の斜辺をc, 他の2辺をa, bとすると c2 = a2 b2の関係が成り立つ。 a b c a b c c 2 = a 2 b 2三平方の定理とは? / 三平方の定理の逆 / 有名角と比 / 2点間の距離 / 円の中心と弦との距離 / 空間図形の対角線・高さ / 空間図形とひもの最短距離




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
三平方の定理(ピタゴラスの定理)の誕生秘話 ピタゴラスはギリシャのサモス島というところで生まれました。このサモス島のヘーラー神殿というところを散策していたときのことです。足元に敷き詰められた下の図ようなタイル貼りを見て、ピタゴラスはあることに気づいたそうです。 実にシンプルな模様です。でも、ピタゴラスはこの模様から と一辺が



三平方の定理




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
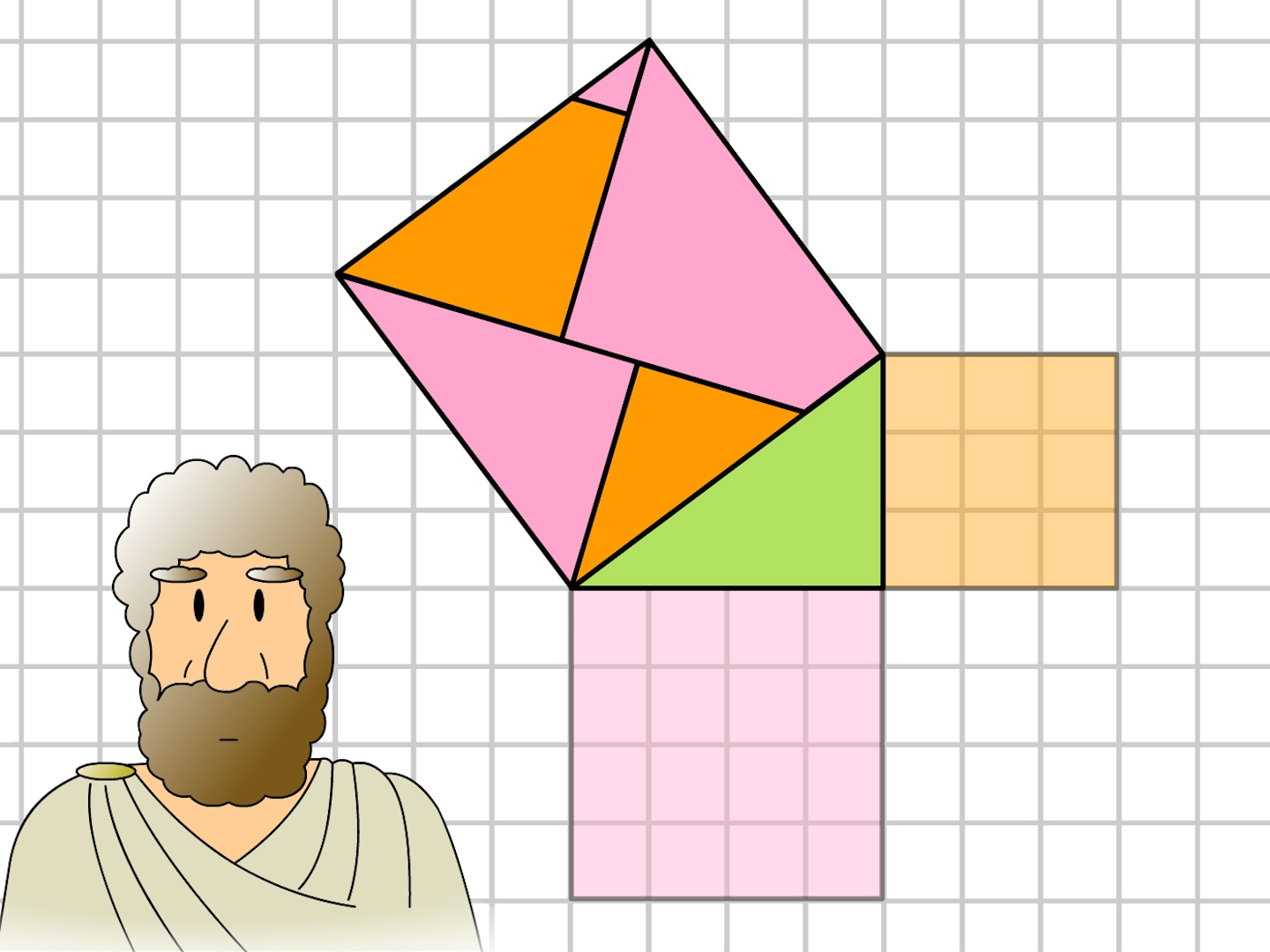



3年 ピタゴラスの定理 数学イメージ動画集 大日本図書




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理 もう一度やり直しの算数 数学




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト



三平方の定理とは コトバンク




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理を英語で読んでみる




ピタゴラスの定理 三平方の定理 ベクター イメージマート




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



見えますか タイルの模様からピタゴラスの定理 Note Board




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



これなら小学生でも分かる 水で車輪を使って ピタゴラスの定理 を証明する実験動画 コモンポストムービー
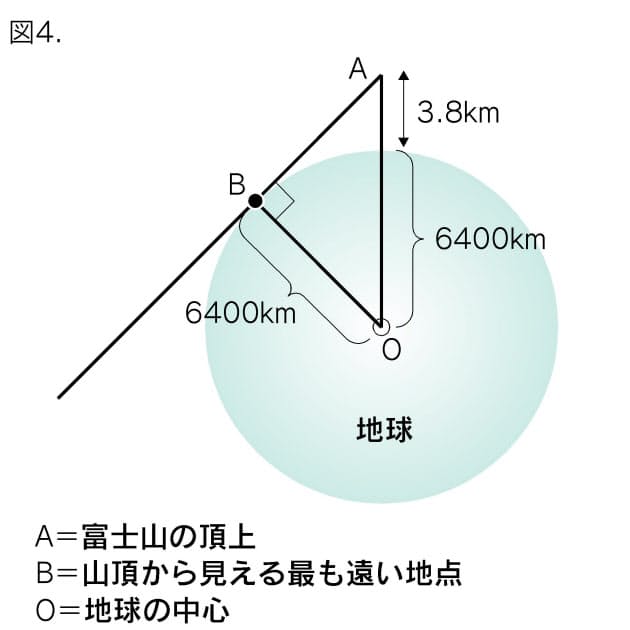



富士山やスカイツリーからどこまで見渡せるか 川の対岸までの距離 渡らずに知る方法 Nikkei Style




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube
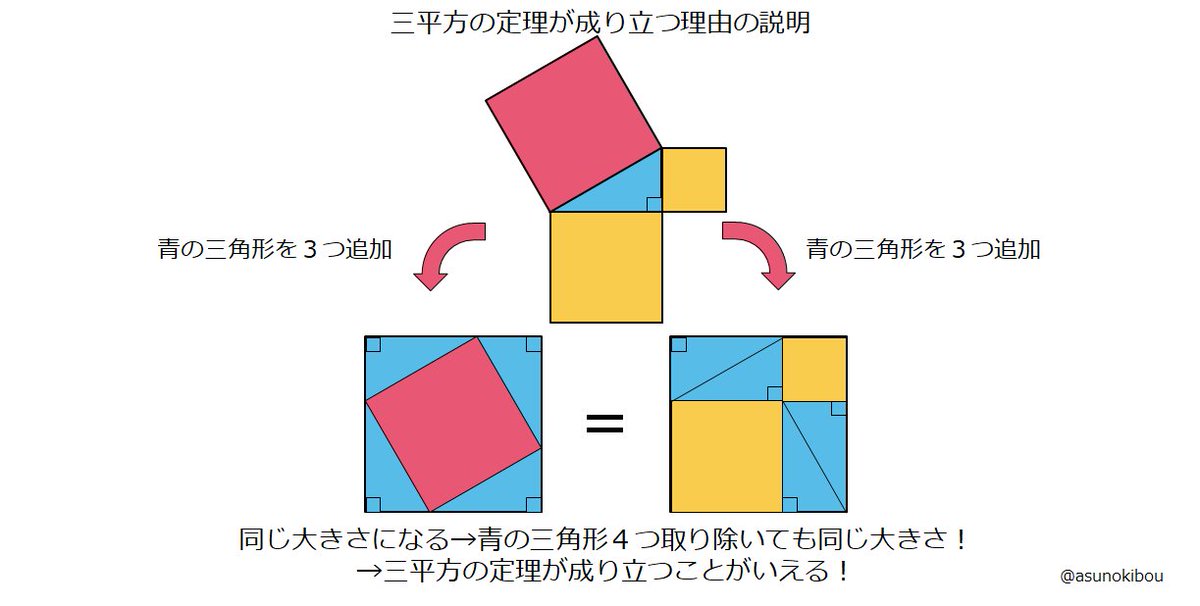



三平方の定理 ピタゴラスの定理 を分かりやすく表した動画 Togetter




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



1




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



1




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース



三平方の定理




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook




ピタゴラスの定理 Wikipedia




三平方の定理 がひと目で分かる展示が面白いと話題に 視覚的にわかる こういうのが学校にあったら ねとらぼ
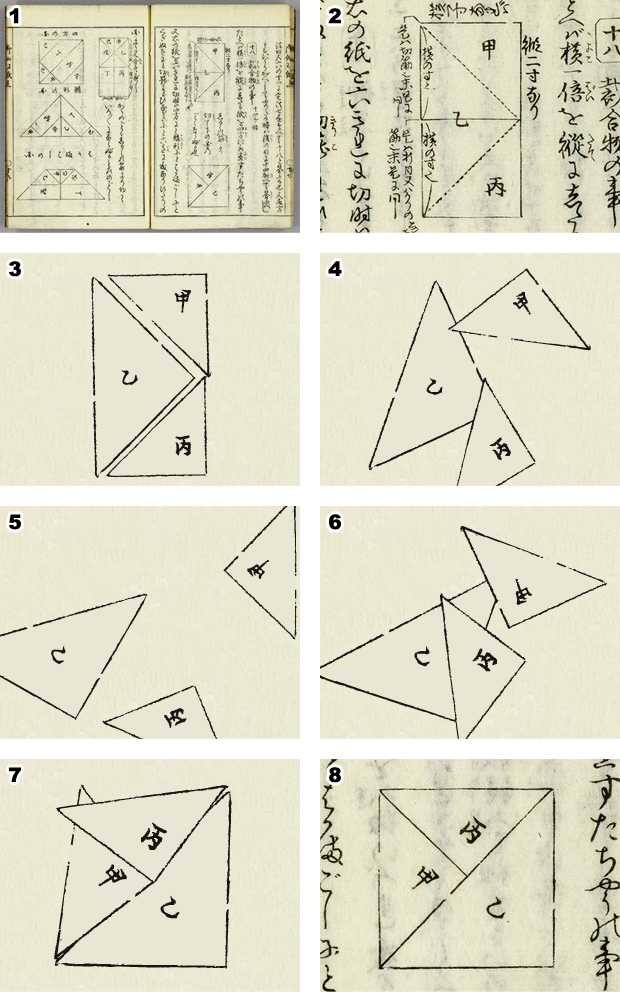



コラム ピタゴラスの定理 江戸の数学




Amazon Co Jp 大人になって知る数学の魅力 三平方の定理 ピタゴラスの定理 から見る数学の美しさ Ebook 賢者企画 本
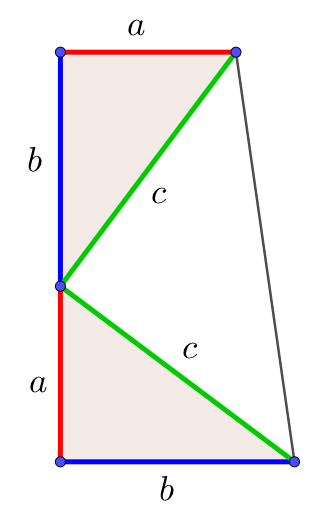



三平方の定理の証明3 大統領の台形 キソカラ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 無料で使える中学学習プリント




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1




数学 中3 61 三平方の定理 基本編 Youtube



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三平方の定理のイラスト素材




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
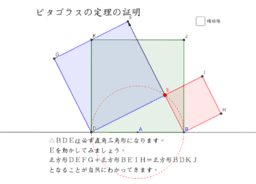



ピタゴラスの定理 三平方の定理 の証明 Geogebra
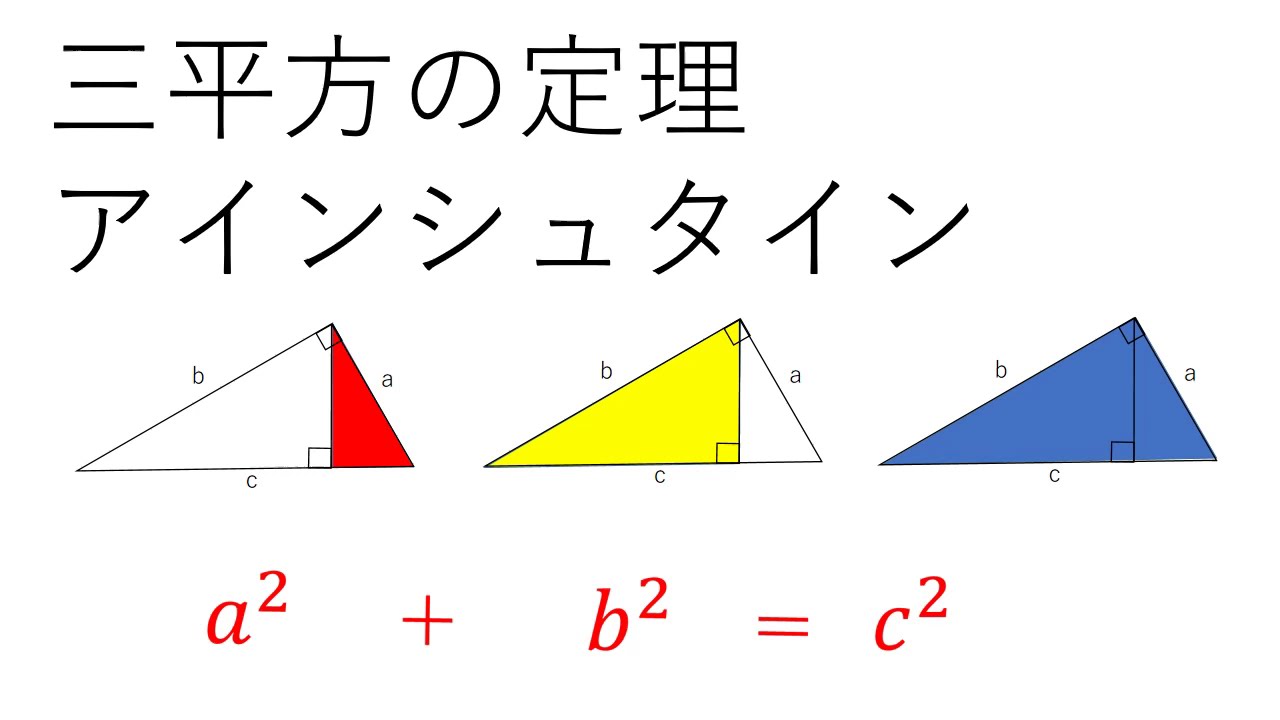



三平方の定理8 アインシュタイン Youtube
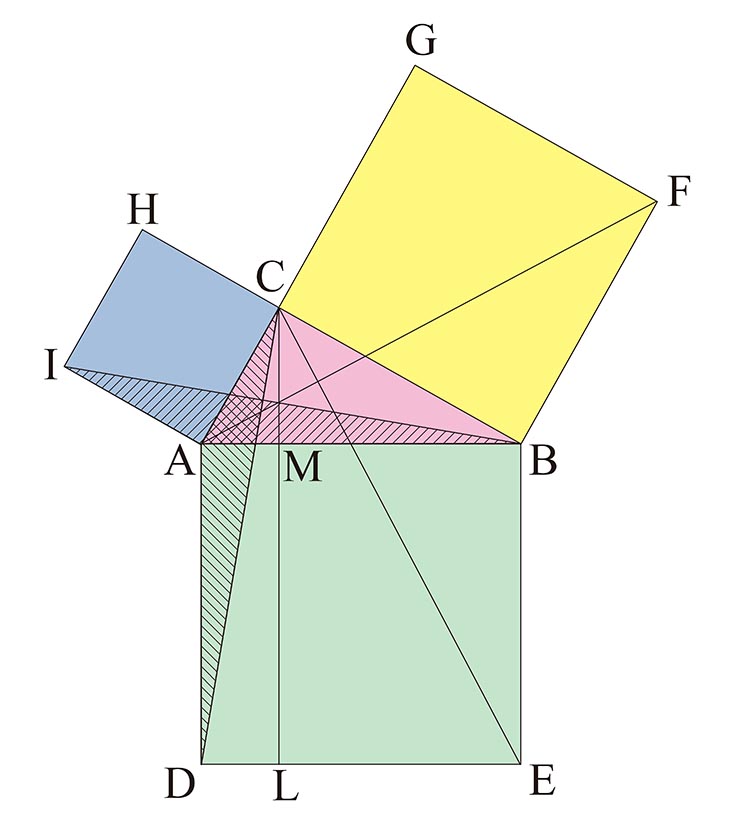



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション




ピタゴラスは遅かった 三平方の定理 最古の応用例 朝日新聞デジタル




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




ピタゴラスの定理 三平方の定理 のイラスト イラスト素材 フォトライブラリー Photolibrary




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理の練習問題10問 解き方の解説 数学fun




三平方の定理で辺を求める Youtube



三平方の定理




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



ピタゴラスの定理とその証明
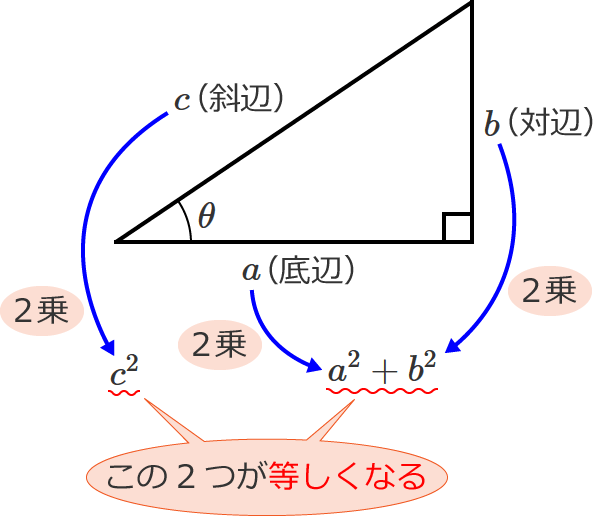



三平方の定理 ピタゴラスの定理
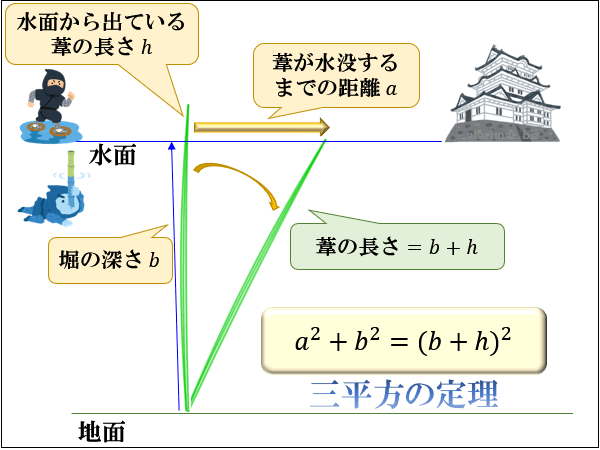



三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
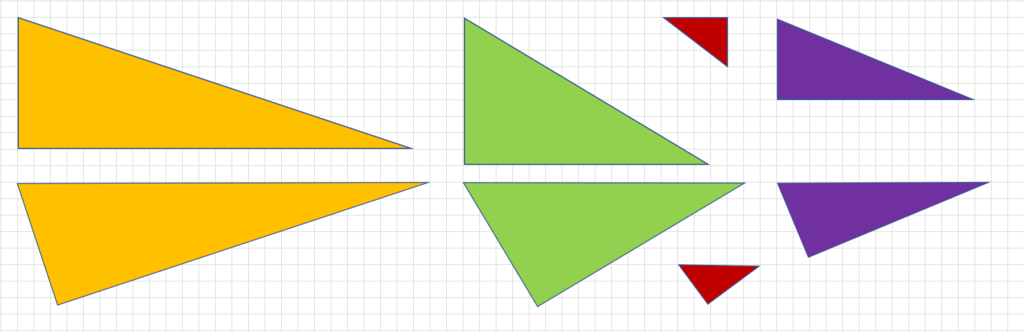



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題
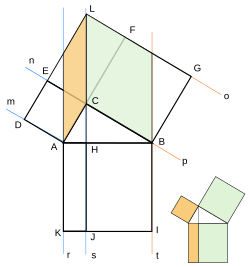



ピタゴラスの定理 Wikipedia




三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生



三平方の定理




三平方の定理 おやじさん ネット



投稿1036




三平方の定理 ピタゴラスの定理




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4



名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 ひ ではじまるキーワード キーワード ピタゴラスの定理 公式と図形




三平方の定理の4通りの美しい証明 高校数学の美しい物語




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook



三平方の定理




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理 自動計算サイト




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
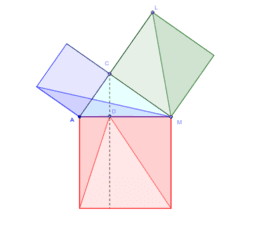



ピタゴラスの定理 三平方の定理 の証明 Geogebra



ベクトルの長さを三平方の定理を使って求める




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理の証明と使い方



0 件のコメント:
コメントを投稿