👍 Correct answer to the question The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?Write a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) areYou can put this solution on YOUR website!
1
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used-Answer 2 📌📌📌 question The identity (x^2y^2)^2 = (x^2y^2)^2 (2xy)^2 can be used to generate pythagorean triples what pythagorean triple could be generated using x=8 and y=3 the answers to estudyassistantcom The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y Skip to Content




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes
When adding and multiplying like terms students may initially confuse x x as x2 instead of 2x factors and can be used to factor polynomials of any power The degree of a polynomial will identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to(x – y) 2 = x 2 – 2xy y 2 LHS = RHS Hence, proved x 2 – y 2 = (x y) (x – y) By taking RHS and multiplying each term (x y) (x – y) = x 2 – xy xy – y 2 (x y) (x – y) = x 2 – y 2 Or x 2 – y 2 = (x y) (x – y) LHS = RHS Hence proved In the same way, you can prove the other above given algebraic identities Problems on Algebraic Identities Problem Solve (x 3) (x – 3) using algebraic identities Solution By the algebraic identity, x 2 How do you use Implicit differentiation find #x^2 2xy y^2 x=2# and to find an equation of the tangent line to the curve, at the point (1,2)?
1 6 x 2 4 y 2 9 z 2 1 6 x y 1 2 y z 2 4 x z Medium View solution Factorise 4 x 4 9 y 4 6 x 2 y 2 Easy View solution Factorise the following, using the identity a 2Write a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less• See x4 – y4 as (x2)2 – (y2)2, thus recognizing it as a difference of squares that can be factored as (x2 – y2)(x2 y2) • In the equation x2 2x 1 y2 = 9, see an opportunity to rewrite the first three terms as (x1)2, thus recognizing the equation of a circle with radius 3 and center (−1, 0)
By using formula (xy)^2 = x^2 y^2 2xy we can solve this problem Now x^2 y^2 = (xy)^2 2xy Simply put the given values in the above equation & you will get the answer 28 The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;Believe me this can't be simplified It can be expanded and multiplied out (x^(2)2xyy)^2 becomes x^44 x^3 y4 x^2 y^22 x^2 y4 x y^2y^2 and then you still have to multiply by (xy) and that can become x^5(5 x2) x^3 y(8 x^26 x1) x y^2(2 x1)^2 y^3 or that can become
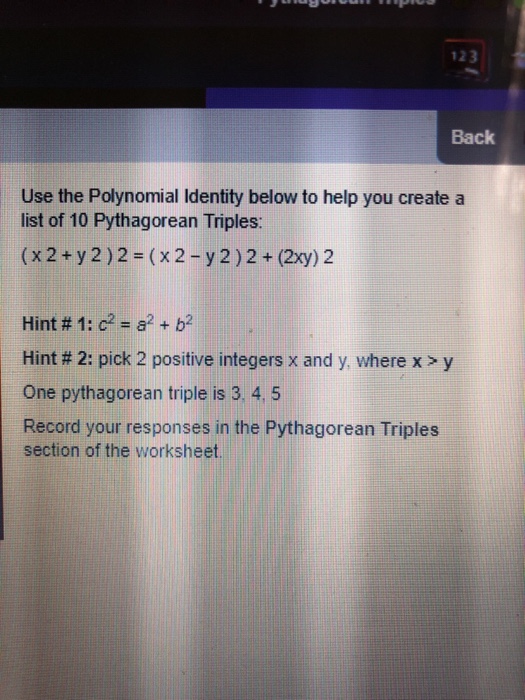



123 Back Use The Polynomial Identity Below To Help Chegg Com




Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube
PreAlgebra Simplify (2xy^22x^3x^2y) (2x^2y2xy^2y^3) (2xy2 2x3 − x2y) − (−2x2y 2xy2 − y3) ( 2 x y 2 2 x 3 x 2 y) ( 2 x 2 y 2 x y 2 y 3) Simplify each term Tap for more steps Apply the distributive propertyFor example, the polynomial identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples I can prove polynomial identitiesAnswer to Verify the identity \bigtriangledown ^2 \vec \text v = \ grad \ div \vec \text v \ curl \ curl \vec \text v for the vector field \vec



If Sin 8 X 2 Y 2 X 2 Y 2 Then Find The Values Of Cos 8 And 1 Tan 8 Sarthaks Econnect Largest Online Education Community




Solving A System Of Equations Using A Matrix Precalculus Socratic
The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could Mathematics, 0640 yo2lo15 The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples$\psi = x^2(y2)^2\lambda(x^2y^21)$ Establish Lagrange Equations $$\psi_x = 2x\lambda(2x)=0 $$ $$\psi_y = 2y4\lambda(2y)=0$$ $$\psi_\lambda = x^2y^21=0$$The polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms;




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Exercise 6 6 Access Free Pdf




3y 2 X b Dx 2y Y 2 3 b Dy 0 Admits An Integrating Factor Which Is A Function Of X Y 2 Mathematics Stack Exchange
An algebraic identity is an equality that holds for any values of its variables For example, the identity ( x y) 2 = x 2 2 x y y 2 (xy)^2 = x^2 2xy y^2 (x y)2 = x2 2xyy2 holds for all values of x x x and y y y Since an identity holds for all values of its variables, it is possible to substitute instances of one side of theFor example, the polynomial identity (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Authors National Governors Association Center for Best Practices, Council of Chief State School Officers Title CCSSMathContentHSAAPRC4 Prove Polynomial Identities And Use Them To DescribeFor example, the polynomial identity (x^2 y^2 )^ 2 = (x^2 – y^ 2 )^ 2 (2xy)^2 can be used to generate Pythagorean triples AAPRC5 () Know and apply the Binomial Theorem for the expansion of (x y)^n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's Triangle




Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2 Cbse Sample Papers




How To Factorise A Polynomial By Splitting The Middle Term A Plus Topper
The Pythagorean triple Identity is (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2, where c = x 2 y 2, a = x 2 y 2, and b = 2xy With x = 3 and y = 5 a = 3 2 5 2 = 16, (this is 16, by the rules x should be greater than y (x > y), in this case √(x 2 y 2) 2 = a) b = 2*3*5 = 30 c = 3 2 5 2For cases where equality is shown using numerical values, (name) will use algebraic operations (eg distributive property, collecting like terms) to prove that the polynomials are equivalentMAFS912AAPR22 In this video, students will use the Polynomial Remainder Theorem to determine whether a linear expression is a factor of a polynomial expression • Internet connection • Speakers/headphones • Computer • Scientific calculator (if necessary) Dividing Polynomials • MAFS912AAPR22 This tutorial can be used to help



Integration For Finding The Arc Length Of Circle X 2 Y 2 A 2 Mathematics Stack Exchange



Www Tau Ac Il Levant Ode Solution 6 Pdf
For ex ample, the polyno mial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples Interpret functions that arise in applications in terms of the context MGSE912FIF4 Using tables, graphs, and verbal descriptions, interpret the key characteristics of a function which models theCan solve it using a simple identity Let's get to the point x y = ?X and y are positive integers;




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Algebraic Expression Nr And Identitie Pdf Free Download
Identities V Last updated at by Teachoo Identity V is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca Let us prove it Proof (a b c) 2 = ( (a b) c) 2 Using (x y) 2 = x 2 y 2 2xyX 2 y 2 2 x 2 y = 1 x 2 − y 2 − 2 x − 2 y = 1 Complete the square for x 2 2 x x 2 − 2 x Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = 2, c = 0 a = 1, b = − 2, c = 0 Consider the vertex form of a parabolaAnd x>y Calculus Find the four second partial derivatives and evaluate each at the given point



Scholarspace Manoa Hawaii Edu Bitstream Differentialequations Pdf




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
X and y are positive integers;Write a(x)/b(x) in the form q(x)By (date), when given a polynomial identity (eg *x^2 y^2 = (x y) (x y)*), (name) will substitute given values (eg *x* = 6 and *y* = 2) and check if both sides of theidentity are equal;



Deohyd Telangana Gov In Wp Content Uploads 09 9 Me2 2 61 To 2 610 Pdf



If Math X Y 2 Text And X 2 Y 2 2 Math What Is The Value Of Math Xy Math Could You Break It Down For Me Quora
For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions 6 Rewrite simple rational expressions in different forms;In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2 Please wait while your changes are saved Create your free accountIf xy = 30 , x^2 y^2 = 61 Using the identity (xy)^2 = x^2 y^2 2xy => (xy)^2 = 61 2(30) => (xy)^2 = 61 60 => (xy)^2 = 1 => (xy) = 1 Therfore the value of xy i
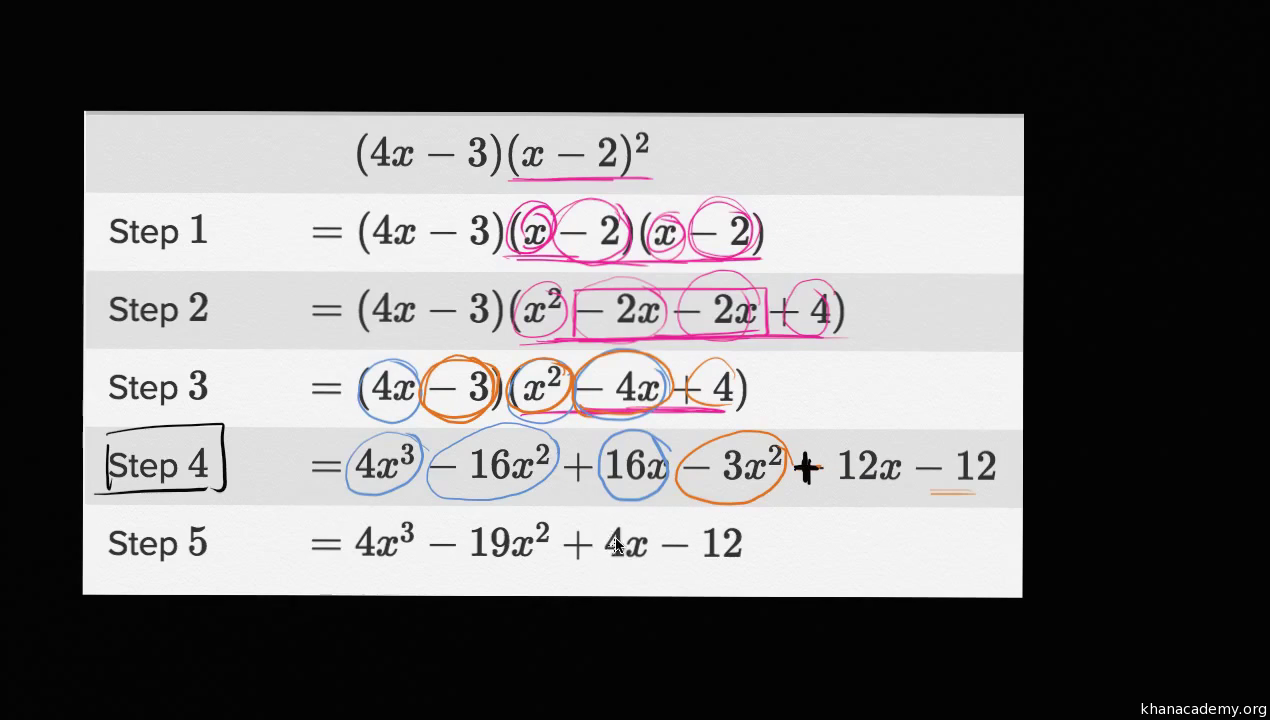



Analyzing Polynomial Identities Video Khan Academy



Polar Coordinates
Identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples A AREI06 Solve systems of equations Solve systems of linear equations exactly and approximately (eg, with graphs), focusing on pairs of linear equations in two variables 22b Solve systems of linear equations andProve polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;




Example 11 Using The Identity I Find I 2x 3y 2 Ii 103 2




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes
The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}2xyx^ {2}=0 y 2 2 x y x 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2x for b, and x^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {2Use the distributive law to explain why x2 – y2 = (x – y)(x y) for any two numbers x and y Derive the identity (x – y)2 = x2 – 2xy y2 from (x y)2 = x2 2xy y2 by replacing y by –y Use an identity to explain the pattern 22 – 12 = 3 32 – 22 = 5 42 – 32 = 7 52 – 42 = 9 Answer (n 1)2 n2 = 2n 1 for any whole number nFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples With the increase in technology and this huge new thing called the Internet, identity theft has become a worldwide problem




View Question A Student Is Asked To Calculate The Pythagorean Triples For The Number 13 Using The Identity X 2 Y 2 2 2xy 2 X 2 Y 2 2 The Student S Steps Are




Algebraic Identities Of Polynomials A Plus Topper
Calculus Basic Differentiation Rules Implicit DifferentiationFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Rewrite rational expressions AAPRD6Students will prove the polynomial identity ( x^2 y^2 )^2 ( 2xy )^2 = ( x^2 y^2 )^2 and use it to generate Pythagorean triples Use this activity as independent/partner practice or implement it as guided notes and practice for students in need of extra support




Jason Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 6 36 Brainly Com




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube
Correct answer The identity (x^2 y^2)^2 = (x^2 y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be genFor example, the polynomial identity (x2 y2)2 = (x2 y2)2 (2xy)2 can be used to generate Pythagorean triples AAPRD Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms;Using identity, (xyz)2 2= x y2z22xy2yz2zx We can say that, x 2 y 2 z 2xy2yz2zx = (xyz) 2 4x 2 9y 16z 2 12xy–24yz–16xz = (2x) 2 (3y) 2 (−4z)(2×2x×3y)(2×3y×−4z)(2×−4z×2x)




Will Give 5 Stars Marshall Uses The Polynomial Identity X Y 2 X 2 2xy Y 2 To Show That 8 Brainly Com
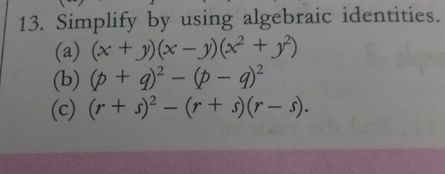



13 Simplify By Using Algebraic Identities Begin Array L Scholr
The polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples SE/TE CB 318 AAPR5 () Know and apply the Binomial Theorem for the expansion of (x y)n in powers of x and y for a positive integer n, where x y are any numbers, with coefficients determined for example by Pascal's Triangle SE/TEAnd x>y (x2−y2)2(2xy)2=(x2y2)2 If the sides of a right triangle are 57, 176, and 185, what are the values of x and y?2) ASSE2 Use the structure of an expression to identify ways to rewrite it For example, see x4 – y 4 as (x2)2 – (y2)2, thus recognizing it as a difference of squares that can be factored as (x2 – y 2)(x2 y2) 3) ASS Choose and produce an equivalent form of an expression to reveal and explain properties
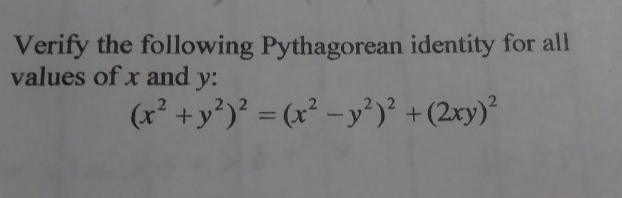



Verify The Following Pythagorean Identity For All Chegg Com




Polar Coordinates
Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 –y 2) 2 (2xy) 2 can be used to generate Pythagorean triples WORKSHEETS RegentsPolynomial Identities AII 11 TST PDF DOC TNS PracticePolynomial Identities sum/difference of cubes 10 WS PDF1 See answer ans is X^2Y^2 = (XY)^22xy AryaBandal is waiting for your help Add your answer and earn points pmtibrahim18pmtibrahim18 x2 y2 can be written as (xy)2 this is in the form of (a b)2 = a2 2ab b2 so the above can be written as x2 2xy y2Use the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is




Given X 2 Y 2 74 And Xy 35 Find The Value Of X Y And X Y



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf
HSAAPRC4 Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2 ) 2 = (x 2 y 2 ) 2 (2xy) 2 can be used to generate Pythagorean triplesFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the




Ex 9 5 2 Use The Identity X A X B X 2 A B X Ab To



Factorize X 2 Y 2 4xz 4z 2 Sarthaks Econnect Largest Online Education Community




Matlab Tutorial




4 08 Polynomial Identities And Proofs By Sheila Bartlett




Facilitator David Brown Ppt Download
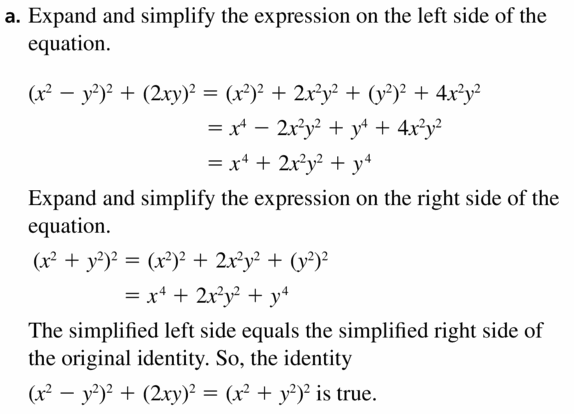



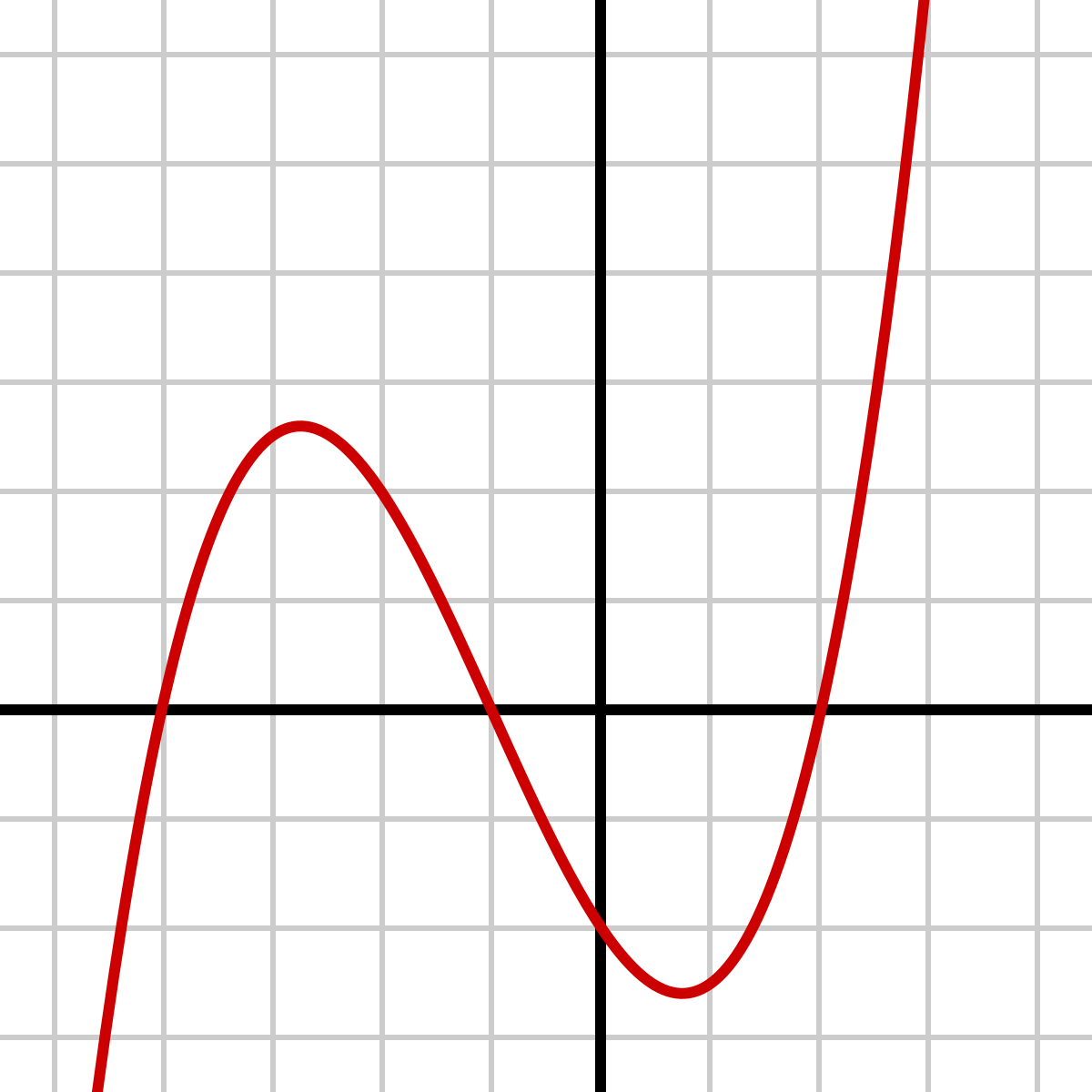
Big Ideas Math Algebra 2 Answers Chapter 4 Polynomial Functions Big Ideas Math Answers




Symmetric Polynomial Identities X Y Z N In Terms Of Sigma 1 X Y Z Sigma 2 Xy Yz Xz And Sigma 3 Xyz Mathematics Stack Exchange



Q Tbn And9gcq8jeckpyefv6nxxng4iwjfl7hsluh Liz05p1lqjy Usqp Cau



Cbse 8 Math Cbse Factorization Ncert Solutions




October 17 Mr Honner



Area Of A Region Bounded By Curves




Welcome Chapter 3 Pairs Of Equations Standard 9




Ppt Polynomials Powerpoint Presentation Free Download Id




Ex 2 5 3 Factorise Following Using Appropriate Identities



Implicit Differentiation




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com




If X Y 2 2 X 2 Y 2 And X Y Lambda 2 4 Lambda 0 Then Lambda Is Equal To




X 2 Y 2 Dx 2xy Dy 0 Novocom Top



Polynomial Wikipedia
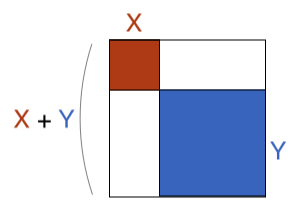



Does Sqrt X 2 Y 2 X Y Brilliant Math Science Wiki




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8




The Pythagorean Triple 5 12 13 Can T Be Generated From The Identity X 1 2 2x 2 X2 Brainly Com
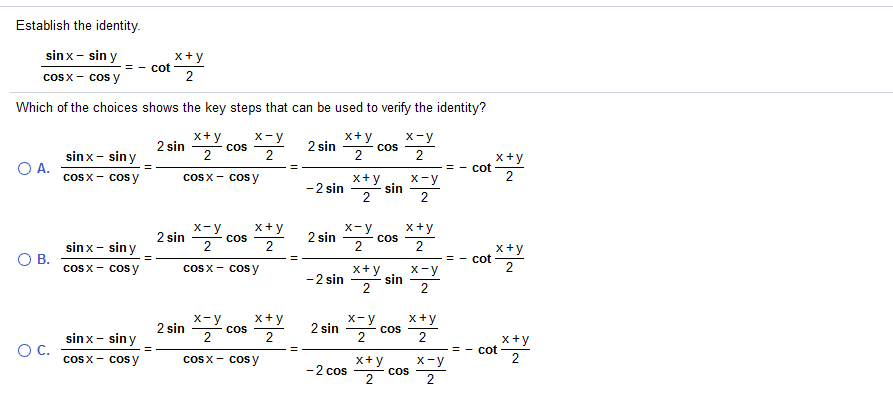



Establish The Identity Sinx Siny X Y Cot Cos X Chegg Com



1



Search Q X2 2b Y2 Formula Tbm Isch




Matlab Tutorial




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is Given By




Maths Activity 2 To Verify Algebraic Identity X Y Z 2 X 2 Y 2 Z 2 2xy 2yz 2zx Math Activities Learning Math Math Concepts




Use An Identity To Factor X2 2xy Y2 1 Maths Polynomials Meritnation Com




X 2 Y 2 Dx 2xy Dy 0 Novocom Top




How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora



Identity Vs Equation Acute Angel




Algebraic Simplification And Evaluation




View Question A Student Is Asked To Calculate The Pythagorean Triples For The Number 9 Using The Identity X2 Y2 2 2xy 2 X2 Y2 2 The



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch17 Pdf




Figure 1 U2 X Y D U 1 X Y Yr X Y Z Dv Xr X Y Z Dv M Yz E Pdf Free Download




Ppt Polynomials Powerpoint Presentation Free Download Id




Is Math X Y 2 X 2 Y 2 Math Or Math X 2 2xy Y 2 Math Quora



How To Simplify Math Frac X 2 2xy Y 2 X 2 2xy Y 2 X 2 Y 2 2 Math Quora




Solving A System Of Equations Using A Matrix Precalculus Socratic




Assignments For Class Xii



X 2 2xy Y 2 X 2 Y 2 2x 2 Xy Y 2 X 2 Xy 2y 2 Youtube




Why Doesn T Math X Y 2 Math Equal Math X 2 Y 2 Math Quora




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube
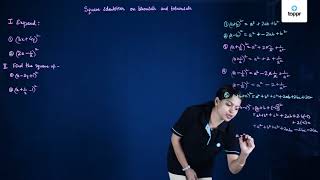



Standard Identities Of Binomials And Trinomials Equations Examples



Multiply X2 4y2 Z2 2xy Xz 2yz By Z X 2y Studyrankersonline




If X 2 Y 2 29 A N D X Y 2 Find The Value Of X Y Ii X Y
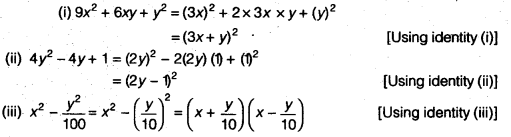



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5




Find The Value Of X2 Y2 Xy Polynomials Maths Class 9




Ex 9 5 1 Use A Suitable Identity To Get Product I X 3 X 3
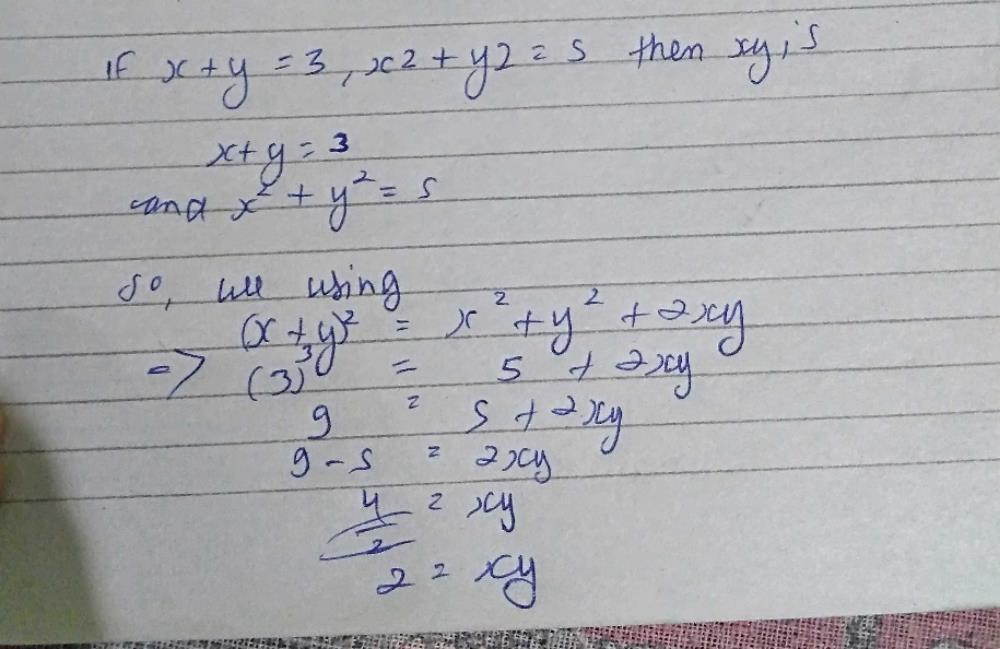



If X Y 3 X2 Y2 5 Then Xy Isa 1b 3c 2d 5correct Answer Is Option C Can You Explain This Answer Edurev Class 9 Question




If X 1 And Y 2 By Using The Identity Find The Following 4 Y 2 9 X 2 16 Y 4 36 X 2 Y 2 81 X 4 And X 2y X 2 2xy 4 Y 2 Snapsolve




Generate Pythagorean Triples Using An Identity Learnzillion




Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2 Cbse Sample Papers



1




Ml Aggarwal Solutions For Class 8 Chapter 10 Algebraic Expressions And Identities Download Free Pdf



Find 2x Y 3z 4x2 Y2 9z2 2xy 3yz 6xz Studyrankersonline




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Polynomials Ppt Video Online Download




Pdf On The Identity Of Fermat S Equation




Teaching Note Supply Tiles For Students A Apr 4 Objective Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example Ppt Download



Cbse 9 Math Cbse Polynomials Ncert Solutions




2 Catherine Was Proving That X2 Y2 2 2xy 2 Chegg Com




X 2 Y 2 Dx 2xy Dy 0 Novocom Top




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Analyzing Polynomial Identities Video Khan Academy



Exponentiation Wikipedia




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




The Vertex Of The Parabola X 2 Y 2 2xy 4x 4y 4 0 Is




44z z2 15 See How To Solve It At Qanda




Rd Sharma Class 9 Chapter 4 Algebraic Identities
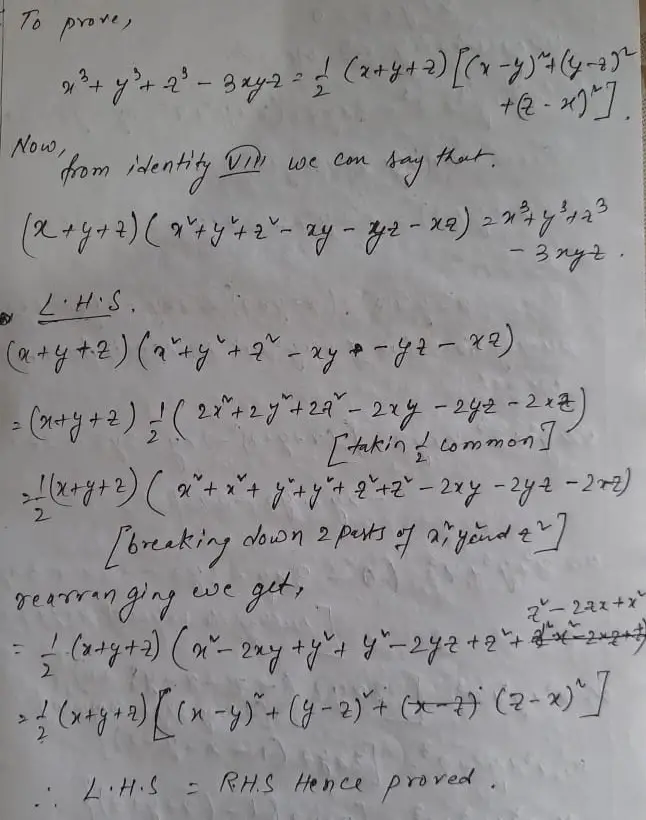



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5



If X Y 4 And Xy 2 Find X2 Y2 Mathematics Topperlearning Com Z4bz3opnn



If X Y 4 And Xy 2 Find X2 Y2 Mathematics Topperlearning Com Z4bz3opnn



0 件のコメント:
コメントを投稿